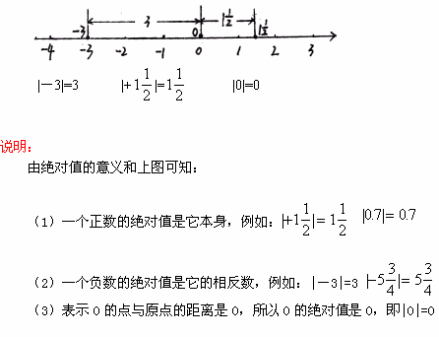
绝对值是指一个数在数轴上所对应点到原点的距离，用“| |”来表示。|b-a|或|a-b|表示数轴上表示a的点和表示b的点的距离。

在数学中，绝对值或模数| x | 为非负值，而不考虑其符号，即|x | = x表示正x，| x | = -x表示负x（在这种情况下-x为正），| 0 | = 0。例如，3的绝对值为3，-3的绝对值也为3。数字的绝对值可以被认为是与零的距离。

实数的绝对值的泛化发生在各种各样的数学设置中，例如复数、四元数、有序环、字段和向量空间定义绝对值。绝对值与各种数学和物理环境中的大小，距离和范数的概念密切相关。

中文名：绝对值

外文名：absolute value

适用领域：数学

所属学科：数学

表达式：| a |

提出者：外尔斯特拉斯

提出时间：1841年

符号：| |

学习时间：高中一年级 初中一年级

关联：数轴

几何意义

在数轴上，一个数到原点的距离叫做该数的绝对值。

应用：|5|指在数轴上5与原点的距离，这个距离是5，所以5的绝对值是5。同样，

绝对值

绝对值

代数意义

正数和0的绝对值是它本身，负数的绝对值是它的相反数。

实数a的绝对值永远是非负数，即

若a为正数，则满足

正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值还是0。特殊的零的绝对值既是它的本身又是它的相反数，写作

任何有理数的绝对值都是非负数，也就是说任何有理数的绝对值都大于等于0。

任何纯虚数的绝对值是就是虚部的绝对值（如：

当a≥0时，

当a<0时，

存在

两个负数比较大小，绝对值大的反而小。

一对相反数的绝对值相等。

计算机语言中，正数的二进制首位（即符号位）为0，负数的二进制首位为1。

32位系统下，4字节数，求绝对值的函数为abs(x)。

无论是绝对值的代数意义还是几何意义，都揭示了绝对值的以下有关性质：

（1）任何有理数的绝对值都是大于或等于0的数，这是绝对值的非负性。

（2）绝对值等于0的数只有一个，就是0。

（3）绝对值等于同一个正数的数有两种，这两个数互为相反数或相等。

（4）互为相反数的两个数的绝对值相等。

（5）正数和0的绝对值是它本身。

（6）负数的绝对值是它的相反数。

绝对值等式、不等式：

（1）若

（2）

（3）

（4）

这个性质一般用在含绝对值的一元二次方程中。

（5）

由此可以得出推论

（1）解绝对值不等式必须设法化去式中的绝对值符号，转化为一般代数式类型来解；

（2）证明绝对值不等式主要有两种方法：

A）去掉绝对值符号转化为一般的不等式证明：换元法、讨论法、平方法；

B）利用不等式：

如果把向南走1公里记为+1，把向北走2公里记为-2，问走了多少公里，计算方法是两个数的绝对值相加，也就是3公里。如果问相对走了多少公里，计算方法是相对数相加，是-1。

如果题中没有说什么是正，如：邮递员送信先向南10米，再向北5米，做题前必须写：记什么为正，一般不用写另一个，因为不是正就是负，知道一个就行了。

利用绝对值可以求两个数中的最大值，公式如下：