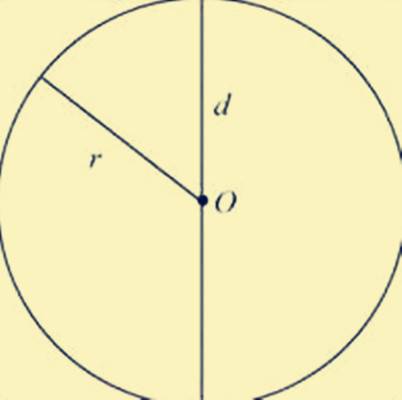
直径(diameter)，是指通过一平面图形或立体（如圆、圆锥截面、球、立方体）中心到边上两点间的距离，通常用字母“d”表示。连接圆周上两点并通过圆心的线段称圆直径，连接球面上两点并通过球心的线段称球直径。

直径是在一个圆中最长的弦。

中文名：直径

外文名：diameter

符号：⌀：读fài，U+2300

应用：几何

别名：经过圆心的弦

学科：数学

计算方法1：直径=半径×2

计算方法2：直径=弧长÷|弧度|×2（仅用在圆中）

直径是通过圆心且两个端点都在圆上任意一点的线段.一般用字母d(diameter)表示。

直径所在的直线是圆的对称轴。

直径的两个端点在圆上，圆心是直径的中点。直径将圆分为面积相等的两部分,中间的线段就叫直径（每一个部分成为一个半圆）。

性质一

在同一个圆中直径的长度是半径的2倍，可以表示d=2r或r=d/2 。

证明：设有直径AB,根据直径的定义，圆心O在AB上。∵AO=BO=r，∴AB=2r

并且，在同一个圆中弦长为半径2倍的弦都是直径。即若线段d=2r（r是半径长度），那么d是直径。

反证法：假设AB不是直径，那么过点O作直径AB',根据上面的结论有AB'=2r=AB

∴∠ABB'=∠AB'B（等边对等角）

又∵AB'是直径，∴∠ABB'=90°（直径所对的圆周角是直角）

那么△ABB‘中就有两个直角，与内角和定理矛盾

∴假设不成立，AB是直径

性质二

在同一个圆中直径是最长的弦。

证明：设AB是⊙O的直径，CD是非直径的任意一条弦，则可证明AB>CD恒成立。

连接OC、OD，根据圆的定义，OA=OB=OC=OD=半径

∵CD不是直径

∴CD不经过圆心O，即O、C、D三点可以构成三角形

在△OCD中，根据三角形三边关系可知OC+OD>CD

∵OA=OB=OC=OD

∴OA+OB>CD

即AB>CD

圆锥曲线直径

园的直径

抛物线的直径

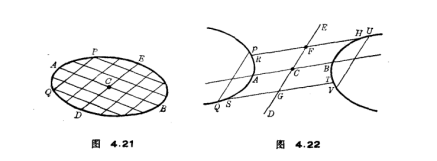
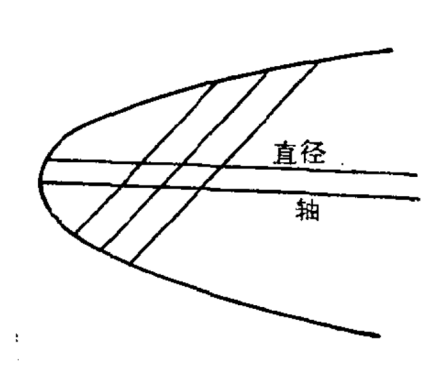
圆锥曲线的平行弦的中点的轨迹，叫做圆锥曲线的直径．

圆的面积公式：半径的平方乘π（即：S=πr^2）